
初当たり確率についての考察です。
要検証。
重要な追記
※数値はバーストエンジェルのものを例として使用
◆とむさん提案の数式
394.74=x+999(1-x)^998+Σkx(1-x)^(k-1)
(Σ→k=2からk=998までの足し算)
◆たけしさん提案の数式
394.74=x(1-{1-(1/x)}^999)
記事内で紹介しているのと同様の方法で解を概算してみたところ……
とむさん提案の数式
→約1/440.08972108
たけしさん提案の数式
→約1/440.08972108
まさかの同じ答えを導けましたw
正直お二人がどういうアプローチでそれぞれの式に至ったのかわかりませんが、同じ答えが出てきたっていうのはかなり心強いですね。
今後の検証対象はこの上記2式にした方が良いかもしれません。
あと、お暇な方がいましたら上記2式が同値であることの証明問題を解いていただけるとありがたいですw
追記ここまで
すろぱちくえすとのだてめがねさんと、パチスロMAXタイプのなおやさんと一緒に、天井到達での当選分を除いた初当たり確率を考える機会がありました。
なんでそんなものを考えたのかはとりあえず置いといて、天井当選分を除いた初当たり確率の計算方法についてバーストエンジェルを例に書いていこうと思います。
注意点として、今から紹介する計算式・計算方法があっているかは自分でもよくわかりませんw
できれば数学が得意な方に検証していただきたいと思ってます。
天井
999G
メーカー発表の初当たり確率
1/394.74(設定1)
考え方(間違ってます)
{本当の初当たり確率}+{天井到達による当選分}
となっているとすると、{本当の初当たり確率}をXと置いた時、{天井到達率}は、(1-X)^999 となる。
{本当の初当たり確率}の{天井到達率}割合だけが{天井到達による当選分}になるので、
{天井到達による当選分}は、X(1-X)^999 。
よって、
1/394.74=X+X(1-X)^999
となる。
※天井到達率の計算を行う際の指数部分は、単純に天井ゲーム数にすればいいというわけではないようですが、今回は煩雑さを避けるために999Gを使って話を進めます。
計算方法・結果(間違ってます)
上記の式が本当にあっているのかはさっぱりわからないので、とりあえずあっているという体で進めますw
最初に書いたように検証して欲しいのは上記の考え方の欄ですので、よかったらお願いします。
で、気になる計算方法ですが、^999が厄介すぎるw
手計算だと無理なんでエクセルさんに泥臭いですが確実な方法で計算してもらいました。
ちなみにこんな感じ↓
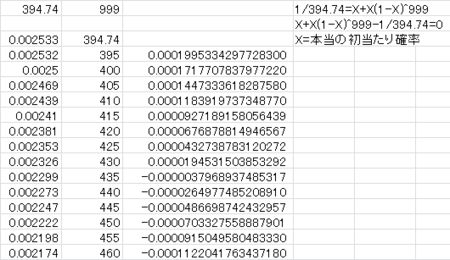
数字がいっぱいで難しそうなことやってるように見えるけど、上で作った方程式のXに適当な数字を代入して、解にあたりをつけているだけです。
適当な数字を代入して、出てきた結果がちょうど±0になればそれが正解だってことですね。
で、出てきた結果は……
約1/434.17でした。(間違ってます)
(※上記追記参照)
何度も言うようですが……
普段なら天井当選分は無視できるレベルなので気にしないのですが、今回の例のバーストエンジェルは天井到達率がめちゃくちゃ高いうえに天井恩恵まであり、無視できないためこういう計算が必要でした。
で、結局は適当に作ってしまった式なので検証して欲しいです。
そこまでズレた値ではないと思うのですが、たぶん間違ってますw
ただ、ここまで計算とかやって気になってきたのは、実はメーカーの発表値は天井当選を含んでないんじゃないかってこと。
もしそうなら今回の計算は無駄という事になりますが……。。。
この辺の規定にも詳しい方いらしたらぜひ教えてください。
ではではノシ


コメント
前からずっと思っていたのでお聞きしたいのですが、天井到達率を計算するときに天井までの残りゲーム数を指数にしますが残りゲーム数-1を指数にするんじゃないんですか?
天井を3ゲーム、初当たり確率を1/2とした場合に8回試行すると、1ゲーム目であたる台が4台、2ゲームであたる確率が2台、3ゲーム目、すなわち天井到達する台が2台となります。
つまり、天井到達率は1/4です。
しかし、(1/2)^3で天井到達率を計算すると天井到達率は1/8となってしまいます。
ここで(1/2)^2で計算すると天井到達率は1/4となりつじつまがあいます。
どっちが正しいのでしょうか。
ほんとですね。今まで気にも留めませんでしたw
おっしゃる通りの方法が良いんじゃないかと思います。
また後で記事も修正しときます。
私も完全に、指数を残りゲーム数から計算してました。
これはちょっと勉強になりました。
いや、こーへいさんの記事にもあっぱれだけど、コメントでこんなに感心するとは思いませんでしたwww
とむさん、こーへいさんお疲れ様です。
>鮭見習いさん
すいません、コメントに埋もれて返信し忘れてましたw
ようやく計算祭も一段落しました(^o^)
この土日月で、受験生みたいな勉強をした気分ですねww
(1-X)^999は999G連続でハズレる確率だと理解できますが、これにXを掛けるのはなぜでしょう?
Xを掛けると実際の初当たり確率を引き、且つ999G連続でハズレる確率って意味になり矛盾が生じます。
だから実際には、
1/394.74=X+(1-X)^999でよいのではないでしょうか?
ちなみにとむさんが言われていることですが、3Gを天井とすると、確率1/2とした場合には3G目は当たろうが外れようが当たるってことになります。
つまり天井Gで即当たる機種のみ-1すればいいと思います。
ただし、天井到達→次ゲームに発動のように前兆がある場合はまた別の話になりますねー
> (1-X)^999は999G連続でハズレる確率だと理解できますが、これにXを掛けるのはなぜでしょう?
(1-x)^999っていうのは、本当の初当たり確率で計算した天井到達率になります。
おっしゃる式を言葉で表してみると、
メーカー発表の初当たり確率=本当の初当たり確率+天井到達率
となってしまいます。
これだと、到達率と初当たり確率という単位?のそろっていない足し算になってしまいますので、嬉しくありません。
(例:本当の初当たり確率1/200、天井到達率5%、みたいな場合に1/200+1/20=メーカー発表値とはなりませんよね)
で、X(1-X)^999 とすることで天井到達率を変換しているつもりですが……
ここがあっているかを検証してほしいですw
指数部分については機種ごとに違うってことでいいですかねw
何度もコメント申し訳ありません
たしかに前兆ゲーム数があったり、そもそも天井ゲーム数が1000とか1600とか大きくなると-1する必要性はあまりなさそうですね・・・
天井100ゲーム、初当たり確率1/100で計算してみました。
ここでいう初当たり確率とは記事内で出てくる{本当の初当たり確率}と同じ意味です。
この条件で計算すると、天井到達率が36.97%で天井を考慮した初当たり確率が1/63.4となりました。
ここで{本当の初当たり確率}である1/100をX+X(1-X)^99-1/63.4に代入すると、-0.002076378924359となりました。
この数値だけでは誤差の範囲なのかどうか分からないので、他の値を代入してみたところ、天井を考慮したさいの初当たり確率が1/82.3としたときの値が+0.0000000379879 となり、ここが値が一番0に近くなりました。
ということは、天井100ゲーム、天井考慮の初当たり確率が1/63.4の場合は{本当の初当たり確率}が1/100なのに対して、X+X(1-X)^99-1/63.4の式で出てきた{本当の初当たり確率}が1/82.3なので、式自体が間違っていると思います。
わかりにくい文章で申し訳ないですが、計算自体は間違えてないと思うのですがどうでしょうか?
連投本当に申し訳ないのですが、上記の条件から天井を考慮した初当たり確率の計算方法は当選ゲーム数×当選台数を1から100まで全て行い試行回数、つまり100でその和を割るといった方法です。
つまり、これを逆に計算していけば{本当の初当たり確率}を求める式が完成すると思い試した結果
{本当の初当たり確率}=A/{1*Ax+2*Ax(1-x)+3*Ax^2*(1-x)^2
+4*Ax^3*(1-x)3+5*Ax^4*(1-x)^4………A*Ax^(A-1)*(1-x)^(A-1)}
となりました。
以上です、長々と失礼しました。
ごめんなさい、訂正です多分僕が考えた式も間違えています。
出なおして来ます。
こんばんは。
なかなか面白い事やってますねー。
天井当選除いた初あたり確率分母*(1-((1-(1/天井当選除いた初あたり確率分母))^天井G数))=初あたり確率分母
って感じで成り立つかなーと自分は思います。
間違ってたらゴメンナサイ^^;
>たけしさん
分数じゃなくて分母部分を使うって発想はなかったですね。
出来れば式の解説して欲しいですw
ともあれ貴重な情報ありがとうございます。
たぶん合ってたっぽいので良かったです^^
文章だと解説しにくいので、また今度会ったときにでも。
本当助かりました(^^)
おおー、ありがたいです。ご指導よろしくお願いしますw
まず1/394.74が本来の当選率での非天井到達時と天井到達時の当選率の合算値とです。
で、たけしさんの式の(1-{1-(1/x)}^999)←この部分は本来の当選率での999G間一度も当選しない確率=”本来の当選率での非天井到達率”という意味です。
本来の当選率*本来の当選率での非天井到達率+本来の当選率*本来の当選率での天井到達率=本来の当選率なので、、、
もう分かりますよね?
解説ありがとうございます(^^)
頑張って理解します。
おっしゃる意味は理解できました。
ただ、いまいちXを掛けるのが腑に落ちないので少し調べてみます
>傀さん
いえ、Xを掛けるのが腑に落ちないのはごもっともです。
自分も計算しときながらイマイチ意味が分かっていませんのでw
検証の協力ありがとうございます!
できました、いろいろ数値を当てはめて検算もしたので間違いないと思います。
A=天井ゲーム数
x=天井非考慮初当たり確率
y=天井考慮初当たり確率分母
A-1
y=x+A(1-x)^(A-1)+kΣx(1-x)^(k-1)
k=2
です。
これで絶対間違いないです。
Σの表記が出来なかったので画像にしました
http://i.imgur.com/riMqgbS.png?1
>とむさん
すいません、式の3項目の部分、
kΣx(1-x)^(k-1)
↓
ΣkX(1-X)^(k-1)
ですよね?(Σの添え字は省略、書き間違いだと思いますが念のため)
意味合いとしては、
A=999
y=400のとき
400=x+2x(1-x)+3x(1-x)^2+…+998x(1-x)^997+999(1-x)^998
って感じですかね?
おそらく一番最後の項を999x(1-x)^998ではなく、999(1-x)^998とするということですよね?
がっつり検証してもらって本当にありがとうございます!
そゆことです!
最後の項は天井なので、Σの式とは分けてるんですよ。
まあ、誰がこんなの計算するんだって話ですけど笑
エクセルでこれが計算できればいいんですけどねー(-_-;)
あと、Σの前にkを持ってきたのはなんか全項にkついてるから括れたよーな・・・みたいな感じでやったので間違ってるかもです。
久々にガッツリ数字をこねくり回せて楽しかったです。
また機会があればこねくり回しに来ます笑
本当に助かりました!
また計算の記事を書くことがあれば是非こねくり回しに来てください笑
はじめまして
自分もいつもエクセル使ってとむさんと同じやり方で出してますね。
天井到達率や平均所要時間計算するときに勝手に出てきます。
しかしスロットはどんどんエナ向きになっていきますね。
個人的にはこういう宵越し以外で天井が隠れない台はあんまり好きじゃないですけどね。
ボーダーは500くらいにしとくつもりですね。
やはり時間効率悪いですしね。
>ぐらさん
おおー、やっぱりこういう計算方法をみんな思いつくんですかね?笑
通常時回す時間がどうしても多くなるんで、時間効率が良い台とは言えないかもしれないですね。
調べて参りましたがどうやら解決済みみたいですね(笑)
一応ほぼトムさんが書かれた式と同義のものとなりました。
こういう数字遊びは楽しいですねー(笑)
わざわざ調べてきていただいたのに申し訳ない(^o^;)
でも、別で計算していた人と同じ式が導けたってだけで心強いです。
偶になら没頭できますけど、自分はもうしばらくはこの遊びしなくて大丈夫ですw
こーへいさんの考えた式も
1/394.74=X+1/394.74(1-X)^999
にすると1/440.0897になりますね。
ホントだ!
これなら自分も努力賞もらえますかね?笑
それにしても、見習いたいくらいのカッコいいフォローをありがとうございます!
ブログ主様へ、
エクセルでの計算式の組み方・または各セルの計算式を教えてはいただけませんか
(Xは天井非考慮の初当たり確率分母)
=X*(1-{1-(1/X)}^天井G数)-公表の初当たり確率分母
この式が丁度0になるようなXを探すという作業をしているだけです。
必要な値を入れればXが一発で求まる式も作れるのかもしれませんが、自分は大して頭が良くないので一つ一つ適当な値を代入してXを求めてます。