確率の問題 (解法求む)

この記事のきっかけはシュタゲ。
ラボメンコンプの確率が求めたかったんですが……。
上記の問題はラボメンコンプを単純化するために自分が適当に作ったものです。
(問題がわかりにくかったら遠慮なく質問してください)

単純そうに見えるんだけど、イマイチ考え方がわかりません。

とっかかりが見えないので知恵をお借りしたいです。

……まさか4*7=28日ってことはないよね？？
(もしそうだったらくだらない記事上げてすみません笑)

大仰な考察がしたいわけではなくて、単に気になってるだけなんで、クイズ感覚でいいので一緒に考えてもらえると嬉しいです。

よろしくお願いします。

追記

正確な答えは求まっていませんが、ごり押しで近似値はわかりました。

約63.78日です。

各日数で観測し終わる確率を直接求めました。

といってもそんなに面倒ではなくて、求める確率には一応法則があったので、さくっとエクセルさんに計算してもらいました。
(式の一般化はできてません。)

【エクセルでの式】
観測日：d
観測週：w
(例えば観測7日目ならw=1週目、観測8日目ならw=2週目)

=(1/4)*(3/4)^(w-1)*{1-(3/4)^w}^{(d-7(w-1))-1}*{1-(3/4)^(w-1)}^{7-(d-7(w-1))}

※7日目だけは0^0が出現するためエラーが出ます。
(0^0を1として処理させれば上手いこと計算できます。)

(与式)
=(1/4)
*(3/4)^(w-1)
*{1-(3/4)^w}^{(d-7(w-1))-1}
*{1-(3/4)^(w-1)}^{7-(d-7(w-1))}

(式の意味)
=その日に雨を観測する確率
*前週までその曜日でまだ雨を観測していない確率
*w週経過した曜日で少なくとも1回は雨を観測している確率
*(w-1)週経過した曜日で少なくとも1回は雨を観測している確率

ちなみにグラフはこんな感じ↓

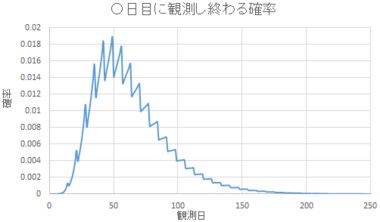
グラフがギザギザしていることからもわかる通り、例えば日曜日から観測を始めたとき、観測し終わる確率が平均的に最も高い曜日は土曜日に、平均的に最も低い曜日は日曜日になるようです。

シュタゲのラボメンコンプも一番左(岡部)で終わる確率が一番低く、一番右(阿万音)で終わる確率が高いといえそうです。

追追記

シュタゲと同じ8Gで1周の条件でも計算してみました。

平均76.29Gとなるようです。

スペシャルムーブを考慮してようやくPV通りのコンプ確率1/69.3くらいになりそう。

つまりこの確率はCZ中の消化G数を含まない確率だということもわかりますね。

《ラックラックライフ・こーへい》